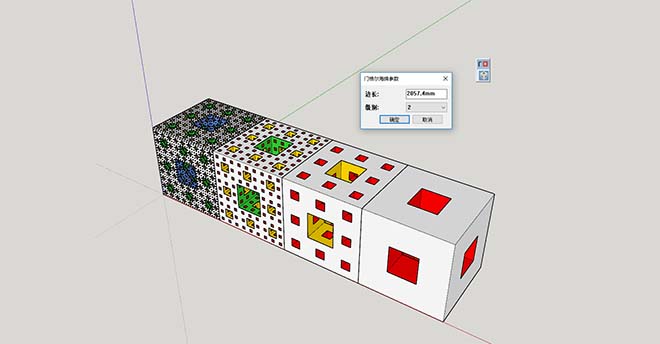
Menger Sponge (门格尔海绵参数) 1.0 -汉化版（优化）Menger Sponge (门格尔海绵参数) 1.0 （汉化）（优化）-1.0.1

插件简介:

这个插件只要输入一个正方形的边长就可以自动生成1-4级门格尔海绵体。

使用教程:

关于孟杰海绵的一些八卦：波兰数学家谢尔平斯基(Vaclav Sierpinski:1882~1969)在1916年提出下图的碎形(fractal)概念，如果把正三角形分成四个小正三角，移除中央倒的正三角形，成一中空三角形。剩余的三个小正三角，再重复同上的细分。如此无限细分下去，得出一像海绵体的东西，每个都由三个小一号（半高）的分身构成。同样的流程也可以运用在正方形、正五边形，或任一种正多边形，甚至于圆形之上。当对立体也如法炮制时，可以得出碎形三角锥；孟结海绵即其立方体的版本，源自其发现者澳洲数学家Karl Menger (1902-1985) ，后来奥地利的数学家Karl Menger延伸出立体的孟杰海绵(Menger sponge)孟杰海绵近似Sierpinski_carpet，将一个正立方体分成3X3X3=27的小立方体像似魔术方块，然后把正立方体的6个面中间的小立方体拿掉，最后将正立方体内最中间的1个小立方体也拿掉，总共剩下20个小立方体，这就是孟杰海绵的最小自我相似单位，以此延续类推，即可产生孟杰海绵。